İntegral Hesaba Giriş: Türler ve Hesaplama
İntegral hesap, integralleri bulmaya ve uygulamalarını incelemeye odaklanır. Isaac Newton ve Gottfried Wilhelm Leibniz, 17. yüzyılın sonlarında bağımsız olarak integral hesabı formüle ettiler. İntegral, integralleri bulmak için kullanılan terim, diferansiyasyonun tersi işlemidir. Kalkülüsün Temel Teoremi hem diferansiyel hem de integral hesabı birbirine bağlar. Entegrasyon kavramı, değişen bir miktarın toplam veya birikmiş etkisini belirleme etrafında döner.
Bu makale, integrallerin tanımlarını, türlerini ve hesaplama tekniklerini kapsayan, çözülmüş örneklerle gösterilen integrallere kapsamlı bir genel bakış sağlayacaktır.
İntegralin Tanımı
Matematikte bir eğrinin altındaki alanı hesaplamak için integral bir kavram kullanılır. Alanı daha küçük parçalara bölmeyi ve yaklaşık bir değer elde etmek için bunları toplamayı içerir. Bu parçaları küçülterek ve küçülterek yaklaşım daha doğru hale gelir. İntegral, bir nesnenin belirli bir süre boyunca kat ettiği toplam mesafeyi hesaplamak için kullanılabilir.
İntegral Türleri
İki ana integral türü vardır:
- Belirli integral
- Belirsiz integral
Belirli integral
Belirli integral, x ekseninde verilen iki uç nokta arasında biriken miktarın tam sayısal değerini bulmak için kullanılır. f(x) fonksiyonunun a’dan b’ye belirli integrali şu şekilde gösterilir:
∫ab f(x) dx.
Belirsiz İntegral (ters türev olarak da bilinir)
Belirsiz integraller, üst ve alt sınırların belirtilmesini içermez. Türevi orijinal fonksiyon olan bir fonksiyon ailesini temsil ederler. f(x)’in belirsiz integrali şu şekilde yazılır:
∫f(x) dx = F(x) + C
Nerede
- ∫f(x) dx, f(x) w.r.t x fonksiyonunun integralini temsil eder.
- F(x), f(x) fonksiyonunun bir anti-türevidir.
- “C” kelimesi integral sabitini ifade etmek için kullanılır.
Kalkülüsün Temel Teoremleri (FTC)
İntegral hesabın temel direklerinden biri Kalkülüsün Temel Teoremidir. Türev ve integral hesabı bu teoremle derinden bağlantılıdır. Bu teoremlerin iki ana bölümü vardır:
Kalkülüsün İlk Temel Teoremi veya FTC1
f(x) [a, b] aralığında sürekli bir fonksiyon olsun ve F(x) bu aralık içinde bu fonksiyonun bir ters türevi olsun. a’dan b’ye fonksiyonun belirli integrali, üst ve alt limitlerde ters türev F(x) arasındaki farka eşittir.
∫ab f(x) dx = F(b) – F(a)
Kalkülüsün İkinci Temel Teoremi
Eğer f(x) [a, b] aralığında sürekli bir fonksiyon ise ve F(x) bu fonksiyonun herhangi bir ters türevi ise. O zaman f(x) integralinin a’dan x’e (x’e göre) türevi, f(x)’in orijinal fonksiyonuna eşittir.
d/dx F(x) = d/dx (∫ab f(x) dx) ⇒ F‘(x) = f(x)
İntegralin Değerlendirilmesi için Formüller
Matematikte integralleri değerlendirmek için kullanılan bazı yaygın formüller şunlardır:
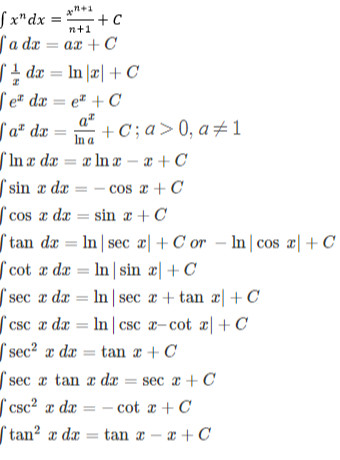
Entegrasyon Teknikleri
İşte birkaç popüler entegrasyon yöntemi:
İkame Yöntemi ile İntegral Bulma
İkame, integral hesapta yeni bir değişken ekleyerek karmaşık integralleri basitleştiren temel bir tekniktir. Bu değişken ikamesi, integrali daha yönetilebilir bir forma dönüştürmeye yardımcı olur. Eğer s u’nun bir fonksiyonu ise, o zaman
s’ = ds/du
∫ f(s) s’ du = ∫ f(s) ds, burada s = g(u).
Parçalara Göre Entegrasyon
Parçalarla integrasyon, iki fonksiyonun bir çarpımının entegrasyonunu basitleştirmek için kullanılan integral hesapta güçlü bir tekniktir. Formül aşağıda verilmiştir:
∫u dv = uv – ∫v du.
Kısmi Kesirler
Rasyonel fonksiyonlarla çalışırken kısmi kesir ayrışması kullanılır. Karmaşık bir rasyonel fonksiyonu daha basit kesirlere böler.
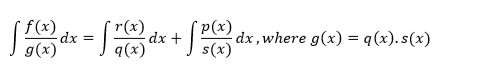
İntegral Uygulamalar
İntegral hesabın yaygın uygulamaları şunlardır:
- Değişim ve birikim oranlarını bulmak.
- İş ve enerji değerlendirmesi.
- Kütle merkezinin hesaplanması.
- Diferansiyel denklemlerle ilgili problemleri çözmek için.
- Olasılık dağılımlarının belirlenmesi.
- Alanları ve hacimleri tanıyın.
Çözümlü İntegral Örnekleri
İntegralleri bulmak için hem ikame yöntemini hem de parçalara göre integrasyonu kullandığımız birkaç çözülmüş problemi inceleyeceğiz.
Örnek 1:
İşlem ∫x sin(x) dx
Çözüm:
∫u dv = uv – ∫v du formülü ile parçalara göre entegrasyon uygulayın.
Izin:
u = x (farklılaşma için seçin)
dv = sin(x) dx (kalan kısım)
Du ve v’yi hesaplayın:
du = dx
v = -cos(x)
∫x sin(x) dx = x (-cos(x)) – ∫ (-cos(x)) dx
Sadeleştirmek:
– x cos(x) + ∫cos(x) dx
Kalan kısmı entegre edin:
– x cos(x) + sin(x) + C
∫x sin(x) dx = – x cos(x) + sin(x) + C
Örnek 2:
∫2x değerlendirin. √(x2 + 1) dx
Çözüm:
s = x2 + 1 olsun, o zaman ds/dx = 2x olsun, bu da 2xdx = ds anlamına gelir.
İntegral şu hale gelir:
∫2x. √(x2 + 1) dx = ∫ (√s) ds
= ∫ (ler) 1/2 DS
Biliyoruz ki
∫ x n dx = ( xn+1 / (n + 1)) + C
∫ (s) 1/2 ds = [s (1/2) +1 / ((1/2) +1)] + C
= [s3/2/ (3/2)] + C
= (2/3) s3/2 + C
∴ s = x2 + 1
∫2x. √(x2 + 1) dx = (2/3) (x2 + 1)3/2+ C
Verilen fonksiyonun integralinin sonucunu kısa sürede adımlarla almak için Meracalculator ‘ın çevrimiçi integral hesaplayıcısından yardım alabilirsiniz.
Örnek 3:
∫0π/2 cos(x) dx’i değerlendirin
Çözüm:
∴ ∫cos x dx = günah x + C
∫0π/2 cos(x) dx = [sin(x)] 0π/2
Üst ve alt limitlerde değerlendirin:
= günah (π/2) – (günah 0)
= 1 – 0
= 1
= 2
∫0π/2 cos(x) dx = 1
Son
İntegral hesap fikrini derinlemesine inceledik. Bunun tanımı, çeşitli türlerinin yanı sıra kapsamlı bir şekilde araştırılmıştır. İntegral ve diferansiyel hesabı birbirine bağlayan temel teoreme baktık. İntegral problemlerini çözmek için çok sayıda belirli ve belirsiz integral örneği ile farklı teknikler sağladık.
Bilgisayar ve İnternet Dünyasına Dair Her Türlü Soru veya Sorununuzu Soru Sor sayfamızdan bizlere iletebilirsiniz. Sorularınız En Kısa Sürede Cevaplanacaktır.